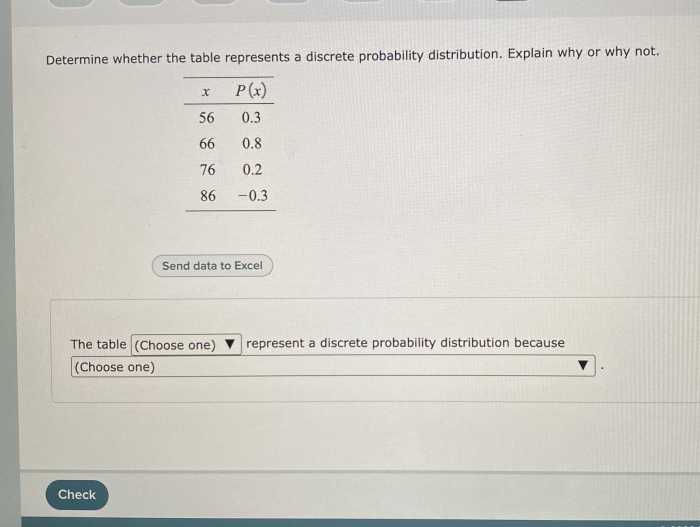
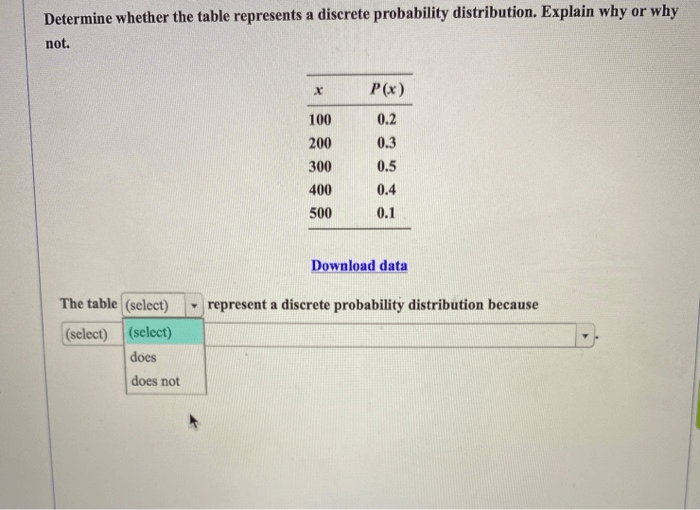
Determine whether the table represents a discrete probability distribution. – The realm of probability distributions encompasses a vast array of concepts, one of which is the discrete probability distribution. In this comprehensive guide, we delve into the intricacies of discrete probability distributions, exploring their definition, properties, and applications.
Discrete probability distributions find their place in various fields, from statistics and finance to engineering and computer science. Understanding their characteristics and how to determine whether a table represents a discrete probability distribution is crucial for accurate data analysis and decision-making.
Definition of a Discrete Probability Distribution
A discrete probability distribution is a function that assigns a probability to each possible outcome of a random variable. Random variables are typically denoted by capital letters, such as X, Y, or Z, and the possible outcomes are denoted by lowercase letters, such as x, y, or z.
The probability of an outcome is denoted by P(X = x), where X is the random variable and x is the outcome.
Discrete probability distributions are used to model random variables that can take on a finite or countable number of values. For example, the number of heads that appear when a coin is flipped is a discrete random variable that can take on the values 0, 1, or 2. The probability of getting 0 heads is 1/2, the probability of getting 1 head is 1/2, and the probability of getting 2 heads is 0.
Properties of a Discrete Probability Distribution
Discrete probability distributions have several important properties:
- The sum of the probabilities of all possible outcomes is equal to 1.
- The probability of any one outcome is greater than or equal to 0 and less than or equal to 1.
- The probability of an outcome occurring is equal to the sum of the probabilities of all the outcomes that are less than or equal to that outcome.
These properties ensure that discrete probability distributions are valid probability distributions.
How to Determine if a Table Represents a Discrete Probability Distribution
To determine if a table represents a discrete probability distribution, you need to check that the table satisfies the following properties:
- The table must have a finite or countable number of rows.
- Each row in the table must represent a possible outcome of a random variable.
- The sum of the probabilities in the table must be equal to 1.
If a table satisfies these properties, then it represents a discrete probability distribution.
Applications of Discrete Probability Distributions
Discrete probability distributions are used in a wide variety of applications, including:
- Modeling the number of successes in a sequence of independent experiments.
- Modeling the number of defects in a manufactured product.
- Modeling the number of customers who visit a store on a given day.
Discrete probability distributions are a powerful tool for modeling random variables that can take on a finite or countable number of values.
Extensions of Discrete Probability Distributions, Determine whether the table represents a discrete probability distribution.
There are a number of extensions of discrete probability distributions that are used to model more complex random variables. Two of the most common extensions are the binomial distribution and the Poisson distribution.
The binomial distribution is used to model the number of successes in a sequence of independent experiments. The Poisson distribution is used to model the number of events that occur in a fixed interval of time or space.
These extensions of discrete probability distributions are used in a wide variety of applications, including:
- Modeling the number of defective items in a batch of products.
- Modeling the number of phone calls that a call center receives in an hour.
- Modeling the number of accidents that occur on a highway in a year.
Extensions of discrete probability distributions are a powerful tool for modeling random variables that can take on a finite or countable number of values.
Commonly Asked Questions: Determine Whether The Table Represents A Discrete Probability Distribution.
What is the key characteristic of a discrete probability distribution?
A discrete probability distribution assigns probabilities to individual values of a random variable, and the sum of these probabilities equals 1.
How can I determine if a table represents a discrete probability distribution?
To determine if a table represents a discrete probability distribution, check if the values in the table are non-negative, the sum of the probabilities equals 1, and each value corresponds to a distinct outcome.